7 Примеры моделирования упругих тел в ПК EULER

Поперечные колебания консольного стержня
Для того, чтобы использовать КЭ модель в качестве упругого звена в Euler, необходимо такую модель заранее создать и рассчитать в специализированном программном пакете. Результат расчета представляется определенным файлом формата «*.mnf», который содержит информацию об интерфейсных узлах и обобщенных формах.
Рассмотрим алгоритм формирования mnf-файла на примере балки, созданной в КЭ комплексе ANSYS. Для наглядности сделаем это несколькими способами, с разными типами элементов: балочным (beam188), оболочечным (shell181) и твердотельным (solid185).
Геометрия балки приведена на рис.13.
 
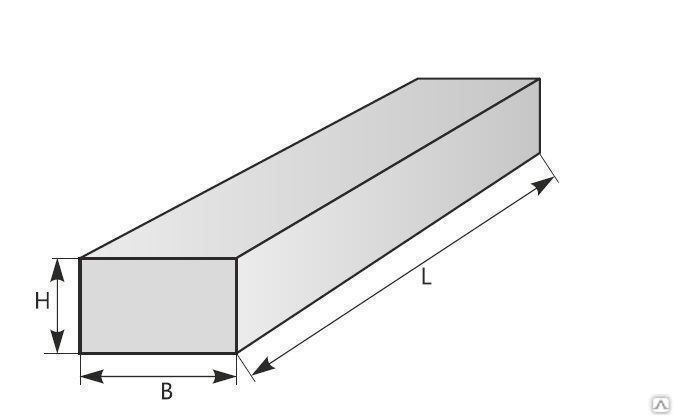
Рис. 13. Геометрия балки
 
Параметры балки, принятые в расчетах следующие:
L=1 [m] – длина балки;
B=0.04 [m] – ширина балки;
H=0.02 [m] – толщина балки;
E=1.5 106 [Pa] – модуль упругости материала;
mu=0.3 – коэффициент Пуассона;
ro=1500 [kg/m3] – плотность материала балки.
Геометрия для каждой КЭ модели была построена в ANSYS
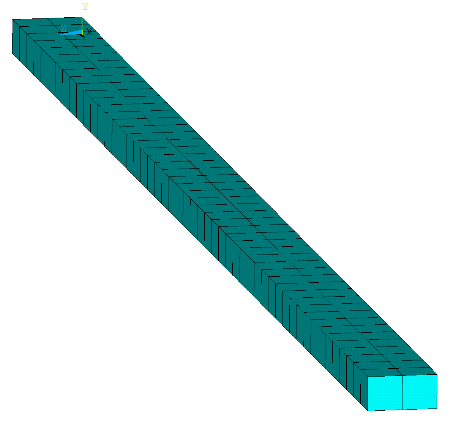
MAPDL 18.2. Далее была сгенерирована сетка. Отметим, что допускается возможность импорта геометрии с конечно-элементной сеткой из ANSYS Workbench. Для балочного и оболочечного типов элементов зададим характерный размер КЭ L / 50, а для твердотельного L / 150, чтобы количество элементов по толщине было больше 2, это увеличит точность расчета. На рис.14 показан внешний вид, полученных моделей.
 
 
а) beam188
б) shell182
в) solid185
Рис. 14. КЭ модели балок
Формирование mnf-файлов проведено согласно подразделу «Генерация файлов в КЭ комплексах для ПК EULER». Создание упругого звена на основе КЭ модели выполнено согласно главе «Импорт редуцированной модели в ПК EULER».
Для конечно-элементной модели используется диагональная редуцированная матрица демпфирования с диагональными элементами равными коэффициенту затухания 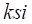=0.1. Число собственных колебательных форм, используемых в расчете – 12. Расчеты были проведены на основе mnf-файлов, полученных для следующих типов конечных элементов:
−      балочный (beam188);
−      оболочечный (shell182);
−      твердотельный (solid185) с интерфейсными узлами, образованными методом «паутины»;
−      твердотельный (solid185) с интерфейсными узлами, образованными методом ограничения перемещений.
Задача о колебаниях консольного стержня решена в следующей постановке: свободный конец балки отклоняется от первоначального равновесного положения сосредоточенной силой в поперечном направлении на небольшое расстояние, после чего сила убирается, что вызывает колебания. Схема закрепления и примерная форма колебания стержня показаны на рис.15.
График перемещения свободного конца моделей стержня показан на рис.16. На графике приведены перемещения для одной твердотельной модели ввиду практически одинаковых зависимостей. На графике видны затухающие свободные колебания.
 
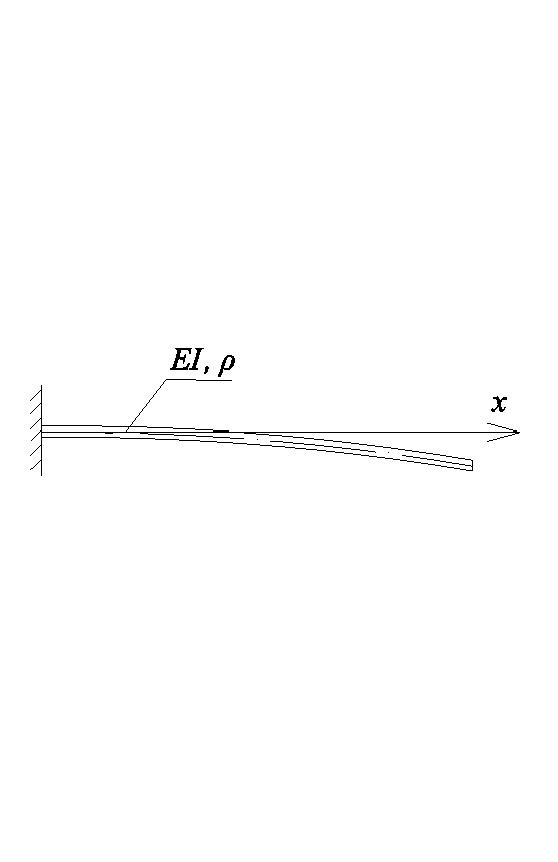
Рис. 15. Примерная форма колебаний консольного стержня
 
 
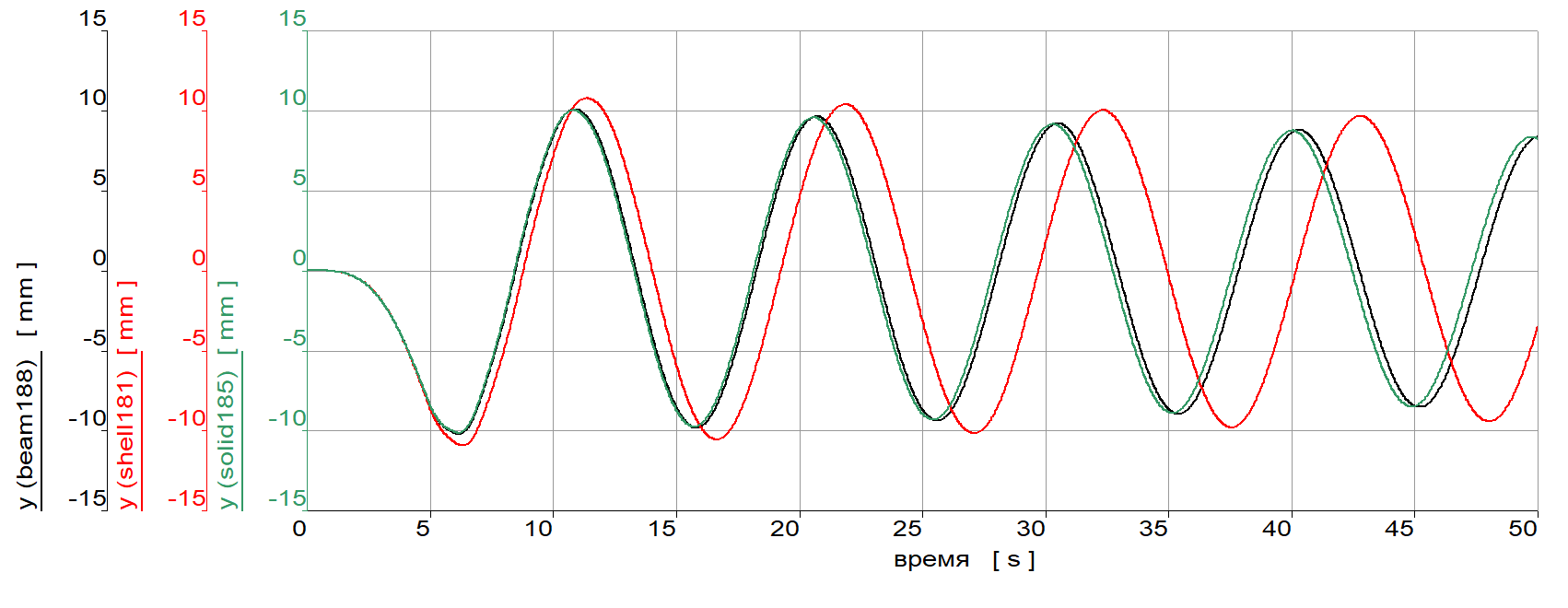
Рис. 16. Перемещения свободного конца моделей стержня
 
Периоды колебаний моделей стержня:
 [s] – балочная модель (beam188);
 [s] – оболочечная модель (shell181);
 [s] – твердотельная модель (solid185) с интерфейсными узлами, полученными методом «паутины»;
 [s] – твердотельная модель (solid185) с интерфейсными узлами, полученными методом ограничения перемещений.
Найдем аналитическое значение периода колебаний стержня и сравним его с полученными нами. Собственные угловые частоты изгибных колебаний однородного стержня определяются следующим выражением:
,
где n =1,2,… - номер собственной формы колебаний стержня;
l – длина стержня;
EJ – изгибная жёсткость стержня;
m – погонная масса стержня;
 - n-е собственное значение.
Для консольной балки первое собственное значение 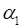=1.875.
Период определим из соотношения 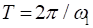. Подставив все значения, получим 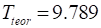[s]. Обратим внимание, что 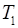,  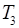и 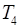 близки по значению с аналитическим решением, а вот  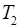отличается существенно. При этом из твердотельных моделей наиболее близкой к аналитическому значению оказалась модель с интерфейсными узлами, полученными методом ограничения перемещений.
Доработаем оболочечную модель стержня. Создадим интерфейсный узел рядом с крайними сечениями и соединим узлы в этом сечении с интерфейсными узлами жесткими невесомыми балками (по аналогии с солидной моделью).
На рис.17 показаны перемещения свободного конца доработанной модели из элементов shell181 (черным цветом) и модели из элементов beam188.
Из рисунка видно, что модели ведут себя одинаково. Период колебаний обновленной модели 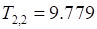[s].
 
 
Рис. 17. Перемещения свободного конца моделей стержня