7 Общая постановка задач идентификации параметров

Идентификация параметров представляет собой задачу определения их значений в модели механической системы, при которых характеристики поведения модели наилучшим образом соответствуют имеющимся результатам измерений функционирования эталонной механической системы. В зависимости от содержательной постановки решаемой задачи под эталонной системой понимается реальная механическая система или некоторый, в том числе теоретический, прототип.
Характеристики функционирования механической системы, используемые для определения соответствия поведения модели и эталона, будем называть характеристиками идентификации или измеряемыми характеристиками. В качестве характеристик идентификации могут служить различные кинематические параметры движения (положения, скорости, ускорения), возникающие силовые воздействия и другие характеристики работы механических систем. В качестве идентифицируемых параметров могут выступать параметры конструкции механизма, задания силовых воздействий, начальных условий движения и другие параметры, оказывающие влияние на процесс функционирования системы.
Задача идентификации решается в следующей постановке.
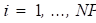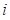−      Имеются результаты измерений характеристик идентификации, полученные в процессе функционирования эталонной механической системы. Эти результаты должны быть представлены в виде функций процесса функционирования системы. Результаты этих измерений обозначим , , где  – -я характеристика идентификации, замеренная в эталонной механической системе; 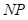– число характеристик идентификации.
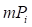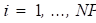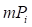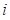−      Имеется представление эталонной механической системы в виде модели ММС. В модели могут измеряться значения тех же характеристик идентификации, что и в эталонной системе. Характеристики в модели обозначим , , где  – -я характеристика идентификации, полученная в модели. Характеристики, полученные в модели, определяются процессом функционирования модели и зависят от значений идентифицируемых параметров.
−      Необходимо определить значения идентифицируемых параметров, при которых полученные в модели характеристики поведения механической системы ближе всего к результатам измерений функционирования эталонной механической системы.
Обозначим вектор идентифицируемых параметров как
,
где 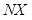 – количество идентифицируемых параметров.
Для идентификации обычно используются данные измерения характеристик системы в процессе ее функционирования. В зависимости от содержательной постановки задачи идентификации они могут быть получены в результате:
−      замеров на одной траектории движения;
−      замеров результатов на совокупности нескольких траекторий движения;
−      замеров характеристик в различных состояниях системы.
Будем считать, что число замеров для всех характеристик идентификации одинаково и равно .
Соответствие поведения модели механической системы имеющимся результатам измерений функционирования эталонной ММС определяется на основе критерия. В качестве такого критерия принимается сумма квадратов расхождений значений характеристик модели и эталона, вычисляемая как
,
где 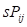 – значение 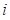-й характеристики идентификации в эталонной механической системе в 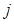-м замере;  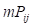– значение 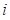-й характеристики идентификации в модели механической системы в том же 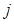-м замере;  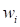– коэффициент эквивалентности 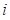-й характеристики идентификации. Размерность  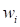должна совпадать с размерностью самой характеристики.
Коэффициенты эквивалентности используются для приведения значений расхождений к безразмерному виду. Значения коэффициентов эквивалентности задаются пользователем. Они определяют относительную важность характеристик для идентификации параметров. Чем больше значение коэффициента эквивалентности, тем менее важна характеристика. То есть, если в модели идентифицируются, например, две характеристики – масса и скорость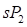, то задание их коэффициентов эквивалентности, как 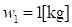и 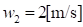означает, что расхождению 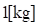, соответствует расхождение скорости .
Таким образом, решением задачи идентификации является вектор значений идентифицируемых параметров 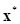, удовлетворяющий условию:
,
где 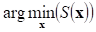 – операция получения значения 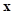, при котором достигается минимум функции .
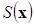Для решения задачи идентификации используются метод наименьших квадратов и модифицированный метод Ньютона. Производные измеряемых в модели характеристик идентификации по идентифицируемым параметрам определяются численным методом.
Решение задачи идентификации считается успешно завершенным в следующих случаях.
1.     Получено совпадение поведения модели механической системы с имеющимися результатами измерений функционирования эталонной механической системы с заданной точностью. То есть, выполнены следующие условия: , ,    .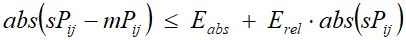
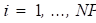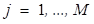2.     Приращения идентифицируемых параметров имеют значения меньше заданной точности. То есть, выполнены следующие условия: 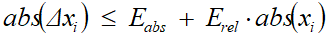, где 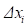 – приращение значения 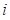-го идентифицируемого параметра, полученное при очередной итерации;  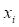– текущее значение 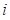-го идентифицируемого параметра.
Задача идентификации решается методом последовательных приближений. В качестве начального приближения используются значения идентифицируемых параметров, установленные в проекте перед началом исследования. Успех решения задачи и скорость сходимости в значительной степени зависят от начального приближения. Поэтому, если задача не сходится, рекомендуется повторить ее решение при других начальных значениях идентифицируемых параметров.
В качестве простого примера задачи идентификации можно привести определение начальных условий бросания камня по характеристикам траектории его движения.
−      Идентифицируемые параметры:
−      начальная скорость;
−      угол бросания.
−      Характеристики идентификации:
−      высота движения камня в зависимости от времени;
−      дальность движения камня в зависимости от времени.
Для решения задачи идентификации в данном случае необходимо выполнить множество замеров значений этих характеристик по траектории.
Для обеспечения удобства работы при решении конкретных задач идентификации могут потребоваться команды, различающиеся по способу формирования результатов замеров, используемых для идентификации. В настоящее время реализована команда “Идентификация параметров по динамике движения”.