7.7 Силы трения в пятне контакта
Силы трения между протектором и опорной поверхностью рассчитываются для каждого дискретного элемента шины. Предполагается, что внутренняя поверхность протектора дискретного элемента связана с кольцом брекера, а внешняя поверхность протектора дискретного элемента связана силами трения с опорной поверхностью. В каждый момент расчета известны положение центра внутренней поверхности протектора дискретного элемента и положение центра внешней поверхности протектора дискретного элемента. Предполагается, что силы трения действуют в плоскости, перпендикулярной вектору силы радиальной деформации элемента. Схема расчета силы трения, действующей на протектор дискретного элемента, представлена на рис.21. Ось X направлена по продольной оси протектора, а ось Y по боковой оси протектора. Текущие (предварительные) деформации продольного и бокового сдвига протектора обозначены на рис.21  и
и 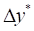 соответственно.
соответственно.
Помимо деформаций продольного и бокового сдвига протектора на силу трения влияют следующие параметры:
−  – коэффициент трения скольжения между материалом протектора и опорной поверхностью;
– коэффициент трения скольжения между материалом протектора и опорной поверхностью;
− 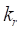 – относительный коэффициент трения покоя (отношение коэффициента трения покоя к коэффициенту трения скольжения);
– относительный коэффициент трения покоя (отношение коэффициента трения покоя к коэффициенту трения скольжения);
− 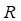 – значение силы радиальной деформации элемента с учетом упругой и демпфирующей компоненты;
– значение силы радиальной деформации элемента с учетом упругой и демпфирующей компоненты;
− 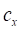 – жесткость продольного сдвига протектора дискретного элемента;
– жесткость продольного сдвига протектора дискретного элемента;
−  – жесткость бокового сдвига протектора дискретного элемента;
– жесткость бокового сдвига протектора дискретного элемента;
− 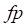 – переменная статуса трения, принимающая три значения, No нет трения, Rest трение покоя, Slide, обозначающий наличие скольжения.
– переменная статуса трения, принимающая три значения, No нет трения, Rest трение покоя, Slide, обозначающий наличие скольжения.
Коэффициент трения покоя между материалом протектора и опорной поверхностью:
Сила трения определяется следующей последовательностью вычислений.
Определяется предварительное значение вектора силы трения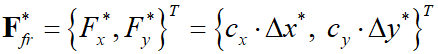 .
.

Рис. 21. Схема расчета силы трения, действующей на протектор дискретного элемента шины
На рис.21 отмечены:
− 1 – положение центра внутренней поверхности протектора дискретного элемента;
− 2* – предварительное положение центра внешней поверхности протектора дискретного элемента;
− 2 – скорректированное положение центра внешней поверхности протектора дискретного элемента.
Для проверки на удержание силами трения имеющегося положения центра внешней поверхности протектора вычисляется предельная сила трения, которая зависит от наличия или отсутствия проскальзывания на предыдущем шаге расчета:
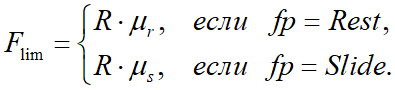
Если выполняется следующее условие удержания силами трения имеющегося положения центра внешней поверхности протектора
то принимается, что сила трения
и имеющееся положение центра внешней поверхности протектора на опорной поверхности остается неизменным для следующего шага расчета.
Если же условие (29) не выполняется, то считается, что произошел срыв центра внешней поверхности протектора и сила трения равна силе трения скольжения по абсолютной величине. Принимаем, что скольжение происходит по направлению силы трения, которая в каждом положении 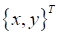 равна
равна 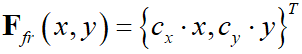 . Траектория скольжения определяется дифференциальным уравнением:
. Траектория скольжения определяется дифференциальным уравнением:
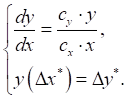
Данное дифференциальное уравнение имеет аналитическое решение:
 .
.Скорректированные значения деформаций дискретного элемента определяются из условия:
Таким образом искомое скорректированное значение продольной деформации 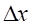 может быть найдено как решение алгебраического уравнения:
может быть найдено как решение алгебраического уравнения:
Итоговая сила трения равна:
где 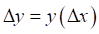 .
.
На основе скорректированных значений деформаций 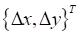 определяется новое положение центра внешней поверхности протектора дискретного элемента, которое будет использоваться для расчета трения для следующего элемента протектора в модели колеса «шина-EULER-M1» и для следующего шага расчета в моделях колеса «шина-EULER-M2» и «шина-EULER-M3».
определяется новое положение центра внешней поверхности протектора дискретного элемента, которое будет использоваться для расчета трения для следующего элемента протектора в модели колеса «шина-EULER-M1» и для следующего шага расчета в моделях колеса «шина-EULER-M2» и «шина-EULER-M3».
Мощность трения скольжения элемента протектора в контакте шины с опорной поверхностью вычисляется как 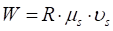 , где
, где 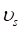 – скорость скольжения, которая может быть вычислена по формуле
– скорость скольжения, которая может быть вычислена по формуле 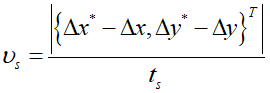 , где
, где 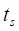 – длительность процесса скольжения.
– длительность процесса скольжения.
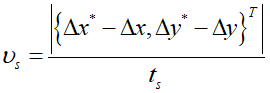 , где
, где