6 Краевая задача

Краевая задача представляет собой задачу определения значений варьируемых параметров, при которых выполняются заданные условия. В качестве условий используется равенство характеристик функционирования ММС заданным значениям. Количество условий может быть любым, но не должно превышать числа варьируемых параметров. Возможно также задание ограничений на значения характеристик функционирования ММС. Количество ограничений может быть произвольным.
Для решения краевой задачи используется следующая исходная информация:
−      Варьируемые параметры ММС. Это могут быть параметры конструкции механизма, силовых воздействий, начальных условий и другие характеристики. Варьируемые параметры должны являться объектами типа скаляр (scalar).
−      Условия краевой задачи – выходные характеристики ММС и значения, которым они должны быть равны. В качестве выходных характеристик в условиях краевой задачи могут использоваться различные кинематические параметры движения частей механизма и другие характеристики. Выходные характеристики для условий должны являться объектами типа датчик (sensor).
−      Ограничения – ограничения на различные кинематические параметры движения частей механизма и другие характеристики. Ограничения накладываются только на объекты типа датчик (sensor). Ограничения задаются одним из следующих способов.
1.     В виде условных выражений (условий). Условие должно содержать ограничения на значения датчика. Синтаксис условий описан в подразделе «Логические условия в выражениях» раздела «Использование математических выражений» главы «Работа с программным комплексом» книги «Общее описание программного комплекса».
2.     В виде простых неравенств. Неравенства понимаются как строгие. Простое неравенство представляет собой объект типа датчик и его минимальное и максимальное значения. Если максимальное значение не задано, считается, что значение датчика сверху не ограничено. Если минимальное значение не задано, считается, что значение датчика не ограничено снизу.
Для задания ограничений возможно комбинированное использование способов 1 и 2.
−      Команда расчета процесса функционирования ММС, для которого проводится решение. В качестве такой команды при решении краевой задачи могут применяться Расчет динамики движения, Расчет сил и ускорений, Расчет траектории положений и другие. Для расчета нельзя использовать команды Исследование методом Монте-Карло, Покоординатная оптимизация, Параметрический анализ и команды, в которые они входят.
−      Параметры настройки для работы алгоритма решения краевой задачи. К ним относятся абсолютная и относительная погрешности выполнения условий; максимальное число итераций и шаги для расчета производных выходных характеристик по варьируемым параметрам.
Для решения краевой задачи используется модифицированный метод Ньютона. Производные выходных характеристик для условий краевой задачи по варьируемым параметрам определяются численным методом; для этого используются задаваемые пользователем шаги для расчета производных. Величины шагов для расчета производных фиксируются на время выполнения команды. Расчет завершается и считается успешным, если достигнута заданная точность решения краевой задачи. Для этого должны быть выполнены следующие условия:
,   
где 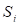 – значение 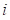-ой выходной характеристики;  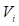– требуемое значение 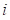-ой характеристики;  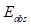– абсолютная погрешность;  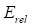– относительная погрешность;  – количество условий краевой задачи.
Краевая задача решается методом последовательных приближений. В качестве начального приближения используются значения варьируемых параметров, установленные в проекте перед началом исследования. Успех решения задачи и скорость сходимости в значительной степени зависят от начального приближения. Поэтому, если задача не сходится, рекомендуется воспользоваться алгоритмом формирования начальных приближений. Для этого необходимо задать:
−      количество начальных приближений;
−      границы изменения варьируемых параметров.
Алгоритм поиска начального приближения работает следующим образом:
−      решается краевая задача из заданной точки;
−      если задача не решена, формируется заданное количество начальных приближений для варьируемых параметров. Начальные приближения выбираются случайным образом в заданных интервалах изменения варьируемых параметров. Выбирается наилучшее приближение, из него решается краевая задача.
Под наилучшим приближением подразумевается следующее:
,   ,   ,
где 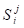 – значение 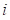-ой выходной характеристики для 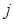-го начального приближения;  – количество условий краевой задачи; 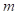 – количество начальных приближений.
Если ограничения заданы, расчет происходит следующим образом:
−      решается краевая задача из заданной точки;
−      если задача не решена или решена, но ограничения не выполнены:
1.     Алгоритм формирования случайных приближений не используется – задача считается нерешенной, выдается диагностика, что не выполнены ограничения;
2.     Алгоритм формирования случайных приближений используется – начальное приближение выбирается следующим образом: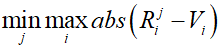, , 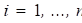  ,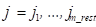, где  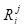– значение 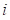-ой выходной характеристики для 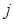-го начального приближения; выходные характеристики  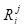являются подмножеством выходных характеристик  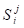(из общей формулы поиска начальных приближений), для которых выполнены ограничения;  – количество условий краевой задачи; 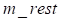 – количество начальных приближений, удовлетворяющих ограничениям. Если ни одно из начальных приближений не удовлетворяет ограничениям, наилучшее приближение выбирается так же, как в случае без ограничений.
В процессе решения задачи для получения значений выходных характеристик в каждой точке значений варьируемых параметров выполняется расчет процесса функционирования ММС. Такой расчет состоит из следующих действий. Проект переводится в режим редактирование. После чего меняются значения варьируемых параметров, и проект переводится в режим исследования. При этом проверяется корректность проекта, и выполняются начальные условия. Затем производится расчет выбранной команды.
Результатом решения краевой задачи является полученный вариант процесса функционирования ММС, при котором выполняются заданные условия и ограничения. Причем вычисляются соответствующие этому варианту значения варьируемых параметров. Кроме того, строятся графики зависимости значений варьируемых параметров, выходных характеристик для условий, ограничений, заданных в виде простых неравенств, и погрешности от номера итерации решения задачи.