6.3 Уравнения связей
Обобщенные силы реакции связей можно выразить согласно уравнению Лагранжа первого рода:
где 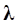 – силовые факторы в связях (множители Лагранжа).
– силовые факторы в связях (множители Лагранжа).
Чтобы выписать выражение для расчета обобщенного якобиана связи 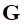 из формулы (31), кратко рассмотрим принципы формирования уравнений связи. Общий вид уравнения связи:
из формулы (31), кратко рассмотрим принципы формирования уравнений связи. Общий вид уравнения связи:
где 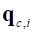 ,
, 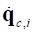 – положения и скорости
– положения и скорости 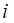 -ой локальной системы координат (ЛСК) связи относительно СКП.
-ой локальной системы координат (ЛСК) связи относительно СКП.
Тогда уравнение для расчета ускорений в связи можно записать в виде (суммирование ведется по всем ЛСК связи):
где 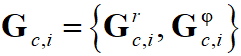 – вектор-строка производных невязок связи по движениям
– вектор-строка производных невязок связи по движениям 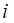 -ой ЛСК связи,
-ой ЛСК связи, 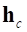 – ускорение нарушения связи при отсутствии ускорения ЛСК связи (
– ускорение нарушения связи при отсутствии ускорения ЛСК связи (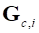 и
и 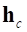 зависит от типа связи).
зависит от типа связи).
Выразив параметры ЛСК через обобщенные параметры тела, с которым она связана, получим:
где 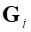 – вектор-строка производных невязок
– вектор-строка производных невязок 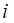 -ой ЛСК связи по движениям соответствующего тела (якобиан связи).
-ой ЛСК связи по движениям соответствующего тела (якобиан связи).
Если 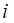 -ая ЛСК связана с абсолютно твердым телом, а центр ЛСК находится в точке
-ая ЛСК связана с абсолютно твердым телом, а центр ЛСК находится в точке 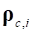 , то в ПСК имеем:
, то в ПСК имеем:
Если 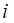 -ая ЛСК связи относится к
-ая ЛСК связи относится к 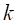 -ому узлу деформируемого твердого тела и отстоит от узла на вектор
-ому узлу деформируемого твердого тела и отстоит от узла на вектор 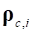 , то:
, то:
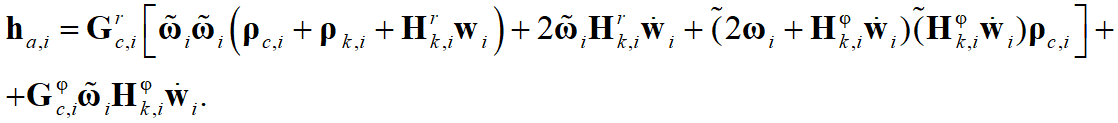
При замораживании деформируемого тела формулы для расчета якобиана наложенной на это тело связи преобразуются в соответствующие формулы для абсолютно твердого тела.