6.2.4 Непотенциальные обобщенные силы и обобщенные силы инерции
Далее рассмотрим непотенциальные (активные) силы, пусть к k-ому интерфейсному узлу приложены сила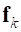 
и момент 
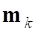в точке, отстоящей от узла на вектор 
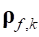. Тогда приложенная сила, приведенная к центру узла, равна 
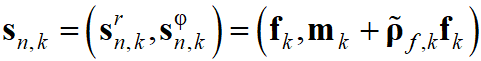и можно показать, что обобщенная активная сила выражается в виде:
и момент в точке, отстоящей от узла на вектор . Тогда приложенная сила, приведенная к центру узла, равна и можно показать, что обобщенная активная сила выражается в виде:
,
, (29)
,
.Таким образом, рассмотрены все члены уравнения Лагранжа (22). Сводя их воедино, получаем уравнение для расчета движения деформируемого звена:
, (30)где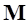 
– обобщенная матрицы масс; 
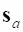– активные обобщенные силы; 
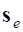– силы упругости; 
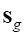– силы тяжести; 
– демпфирующие силы; 
– силы инерции; 
– обобщенные силы реакций связей.
– обобщенная матрицы масс; – активные обобщенные силы; – силы упругости; – силы тяжести; – демпфирующие силы; 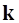– силы инерции; 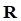– обобщенные силы реакций связей.