6.2.2 Кинетическая энергия, матрица масс, обобщенные силы инерции
С учетом предположения о том, что инерции КЭ модели упругого тела сосредоточена в узлах, запишем соответствующее выражение для полной кинетической энергии:
где 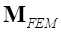 – глобальная матрица масс. В ПК EULER используется только диагональное представление матрицы масс, которое для k-го узла имеет следующий вид:
– глобальная матрица масс. В ПК EULER используется только диагональное представление матрицы масс, которое для k-го узла имеет следующий вид:
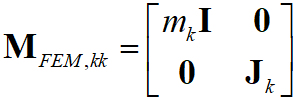 , (19)
, (19)где 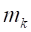 – масса k-го узла,
– масса k-го узла, 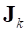 – момент инерции k-го узла.
– момент инерции k-го узла.
Далее с учетом уравнения связи (16) выражение для кинетической энергии в терминах обобщенных координат примет следующий вид:
где 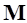 – обобщенная матрица масс. После преобразований, а также принимая во внимание структуру блока матрицы масс для k-го узла (19), получим обобщенную матрицу масс в следующем виде:
– обобщенная матрица масс. После преобразований, а также принимая во внимание структуру блока матрицы масс для k-го узла (19), получим обобщенную матрицу масс в следующем виде:
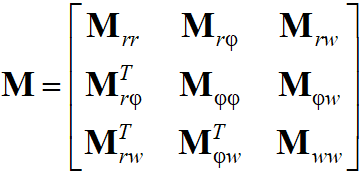 ,
,В формуле (21) и далее подразумевается суммирование по повторяющемуся индексу (индексу форм). Как видим матрица масс состоит из 10 основных блоков, структура которых представлена в виде матричных эквивалентов в таблице 1.
Таблица 1 Инварианты матрицы масс
|
Наименование
блока
|
Структура
блока
|
Размер
блока
|
Количество
блоков
|
Объем данных
блока
|
|
|
|
|
1
|
9
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
1
|
9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
Суммарный объем данных
|
| |||
В ПК EULER реализовано 4 варианта используемых матриц масс, основанных на общей структуре (21) с индивидуальной настройкой для каждого конкретного шаблона упругого тела:
1) Твердое тело – количество форм деформации становится равным нулю, используются блоки 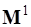 и
и 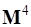 , деформируемое звено, становится эквивалентным жесткому звену.
, деформируемое звено, становится эквивалентным жесткому звену.
2) Формулировка с постоянными членами – в качестве блоков матрицы масс используются эквиваленты, не зависящие от форм деформации: 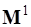 ,
, 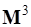 ,
, 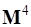 ,
, 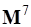 ,
, 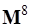 . Таким образом считается, что положение центра тяжести, а также инерционные характеристики деформируемого звена не меняются с течением времени.
. Таким образом считается, что положение центра тяжести, а также инерционные характеристики деформируемого звена не меняются с течением времени.
3) Линейно-связанная формулировка – в качестве блоков матрицы масс дополнительно по сравнению с предыдущей формулировкой используются эквиваленты, зависящие от форм деформации линейно: 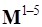 ,
, 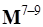 .
.
4) Полностью связанная формулировка – используются все инварианты для достижения наибольшей точности.
Далее, после подстановки формулы (20) и (21) для расчета кинетической энергии и обобщенной матрицы масс в уравнение Лагранжа (11), можно показать, что:
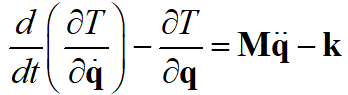 , (22)
, (22)где 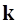 – вектор обобщенных сил инерции, который в ПСК можно записать в виде:
– вектор обобщенных сил инерции, который в ПСК можно записать в виде:
Формулы для расчета обозначенных компонент вектора обобщенных сил инерции выглядят следующим образом:
где 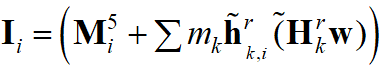 , а столбец матрицы
, а столбец матрицы 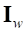 можно выразить в виде
можно выразить в виде .
.