6.2.1 Кинематика деформируемого звена в составе ММС

Для формирования уравнений динамики необходимо на первом этапе выбрать обобщенные координаты, которые будут однозначно определять текущее состояние деформируемого звена. Как уже было сказано ранее движение деформируемого звена рассматривается как сумма большого жесткого движения тела как целого относительно СКП и малых деформаций относительно ПСК (рис.12). Поэтому в качестве обобщенных координат тогда удобно взять совокупность следующих векторов: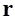

– радиус-вектор текущего положения ПСК;

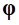– углы определяющие текущую ориентацию ПСК относительно СКП;

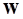– модальные координаты (то же, что и

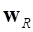в формуле (9)).

Таким образом векторы обобщенных координат и скоростей будут представлены, соответственно, следующим образом:

,

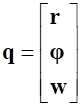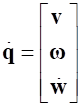. (12)

Аналогичные представления удобно ввести также для положения и скоростей k-го узла:

,

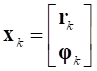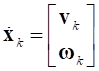. (13)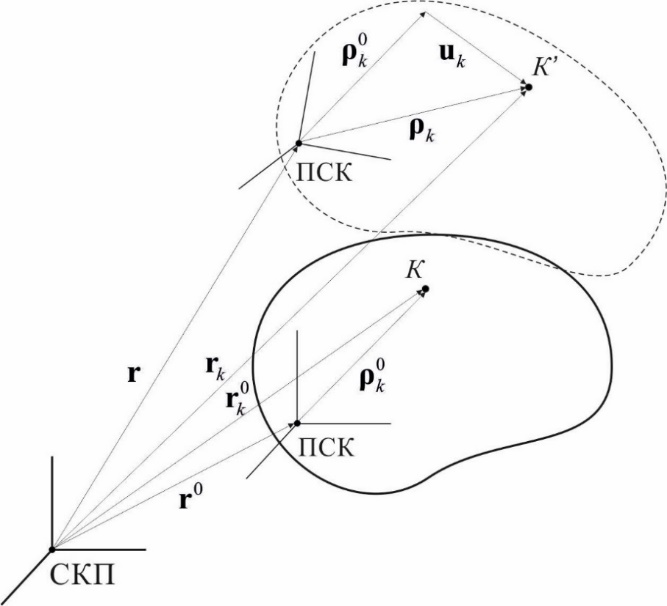

Рис. 12. Описание движение деформируемого звена

Математически связь между положением k-го узла и выбранными обобщенными координаты в терминах ПСК можно выразить следующим образом:

,

, (14)

где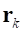

– радиус-вектор k-го узла текущей конфигурации деформируемого звена;

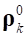– вектор начального положения k-го узла относительно ПСК;

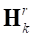– часть модальной матрицы, соответствующая поступательным степеням свободы k-го узла;

– углы, определяющие ориентацию k-го узла текущей конфигурации деформируемого звена относительно СКП;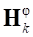

– часть модальной матрицы, соответствующая вращательным степеням свободы k-го узла.

После дифференцирования можно получить аналогичную связь для скоростей k-го узла:

,

. (15)

Или с учетом (12) в матричной формулировке:

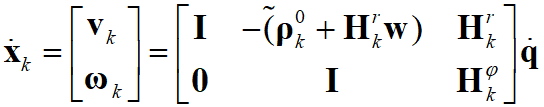. (16)

где знак «~» над трехмерным вектором обозначает операцию взятия кососимметрической матрицы для этого вектора; знак «~» над открывающей скобкой применяется к результату выражения в скобках. Если ввести матрицы

,

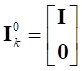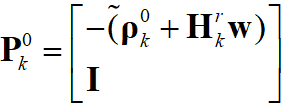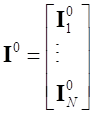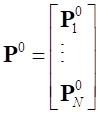, то можно

сформировать аналогичное (16) выражение для всех узлов КЭ модели:

. (17)