6.1 Формы деформации упругого тела

Несмотря на то, что число степеней свободы КЭ модели конечное, оно как правило достаточно большое. Кроме того, значительное количество степеней свободы приводит к появлению в уравнении движения форм деформаций, которые не имеют практического интереса. Поэтому важным аспектом, представляющим собой следствие КЭ дискретизации, является процесс получения форм деформации упругих тел (component mode synthesis). Данный процесс основан на представлении деформации упругого тела в каждый момент времени в виде линейной комбинации более простых форм (рис.11).

, (1)

где u – вектор перемещений размером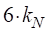

; H – матрица форм деформации; w – набор произвольных модальных координат размера

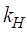. Основным преимуществом подобной трансформации является наличие возможности существенно уменьшать размерность решаемой задачи.

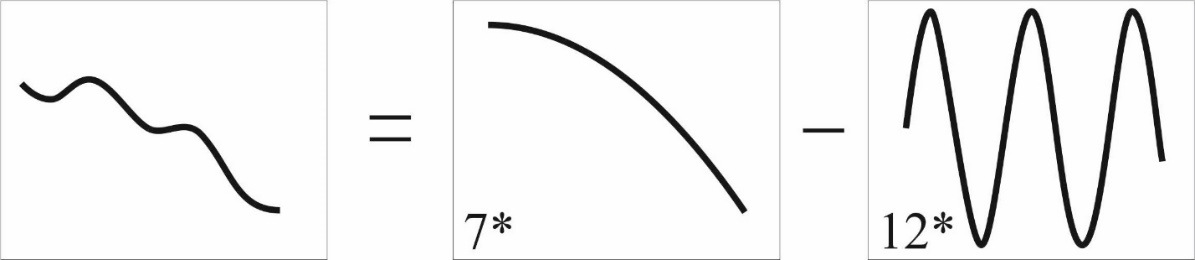
Рис. 11. Линейная комбинация простых форм

В зависимости от вида матрицы H различают методы редукции механических систем. В настоящее время в качестве основного способа редуцирования в ПК EULER используется модифицированные вариант метода Крейга – Бэмптона. Он состоит из пяти основных этапов:

1. Деление узлов на две категории – интерфейсные и внутренние.

В качестве интерфейсных выбираются узлы прикрепления внешних (по отношению к рассматриваемому упругому телу) силовых элементов и шарниров, точки приложения активных сосредоточенных сил, а также любые другие узлы, приближенное представление движения которых не желательно. Все остальные узлы считаются внутренними.

Вектор перемещений, а также матрицы масс и жесткости, полученные с помощью МКЭ, принимают следующий вид:

,

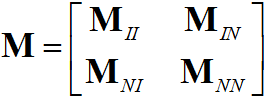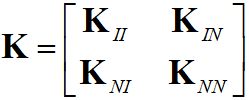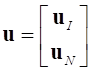где индекс I соответствует интерфейсным (граничным) узлам, а N – всем остальным (внутренним).

2. Расчет статических форм

Статические формы получают в результате единичных смещений в направлении каждой из степеней свободы интерфейсных узлов при закрепленных остальных, что соответствует однородной задаче статики:

.

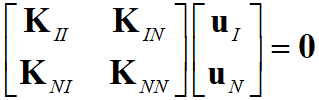Выразим из второй части данного уравнения перемещения прочих узлов через интерфейсные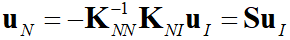

. Таким образом, получим следующее выражение:

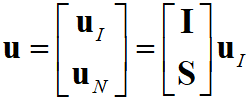, (2)

где I – единичная матрица, S – матрица статических форм. Отметим, что модальные координаты в этом случае в точности соответствуют физическим.

3. Расчет собственных форм колебаний

Рассмотрим обобщенную проблему собственных значений:

, (3)

Поскольку собственные формы колебаний находятся при закрепленных интерфейсных узлах (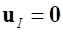

), то размер задачи (3) соответствует количеству степеней свободы внутренних узлов, где

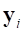– набор собственных форм,

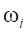– набор собственных частот, соответствующих этим формам. Множество собственных форм удобно скомпоновать в виде матрицы

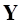, тогда упругие перемещения внутренних узлов можно представить следующим образом:

,

где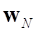

- модальные координаты, соответствующие колебаниям тела. И значит:

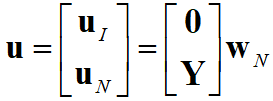, (4)

4. Построение модальной матрицы, матриц масс и жесткости

Из вышесказанного следует, что произвольные малые упругие деформации тела можно аппроксимировать совокупностью найденных статических и собственных форм, выбрав в качестве модальных координат комбинацию выражений (2) и (4), получим:

,

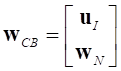размерности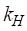

. Тогда тождество (1) согласно классическому методу Крейга – Бэмптона будет иметь следующий вид:

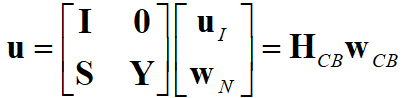, (5)

Покажем выражения для матриц масс и жесткости после редуцирования:

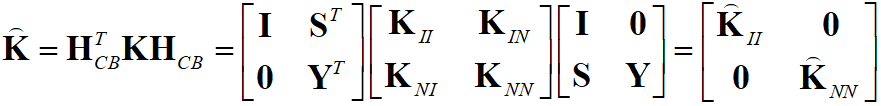, (6)

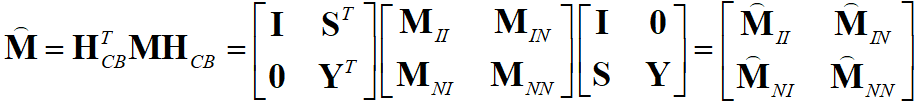, (7)

Матрица жесткости после трансформации является блочно-диагональной. Блоки соответствующих матриц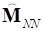

и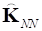

представляют собой диагональные матрицы, а в случае если набор собственных форм

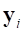ортонормирован относительно

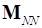, то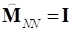

.

5. Ортонормализация базиса модального пространства

Прямое использование матрицы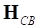

в качестве модальной при расчете динамических систем имеет некоторые недостатки:

− ПК EULER использует свои уравнения для описания больших жестких движений твердого тела, поэтому наличие твердотельных форм в матрице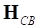

, которые по сути дублируют эти уравнения, приводит к появлению линейной зависимости в строках/столбцах для матрицы масс;

− статические формы в матрице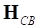

исключать нельзя. Кроме того, так как эти формы есть результат статической конденсации, то непонятно каким частотам при решении задачи динамики они соответствуют;

− блоки матриц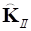

,

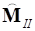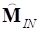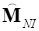все еще остаются плотно заполненными даже после редуцирования.

Изложенные выше проблемы могут быть решены с помощью ортонормализации базиса модального пространства относительно пары редуцированных матриц масс и жесткости. Данная задача сводится к решению обобщенной проблемы собственных значений вида:

, (8)

где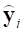

- набор обобщенных форм;

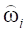- обобщенные частоты, соответствующие формам деформации;

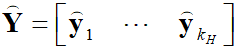- матрица, содержащая множество обобщенных форм, причем

,

где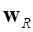

- набор модальных координат базиса, ортогонального исходному.

Так как множество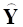

ортогонально относительно

и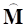

, то после нормализации относительно

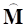получим:

,

где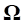

- диагональная матрица. Подставив в последние формулы выражения (6) и (7), получим, что

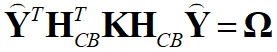и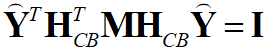

. Если теперь в качестве модальной матрицы принять матрицу

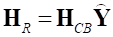, то:

. (9)

Выражение для редуцированных матриц масс и жесткости в таком случае с учетом ортонормализации примет следующий вид:

,

. (10)

В качестве модальной матрицы далее будем всюду использовать матрицу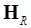

при этом индекс может быть опущен. Тождества (9) означают, что базис модального пространства ортогонален относительно

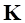и ортонормирован относительно

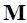. Следует отметить, что полученные формы являются именно результатом ортогонализации модального пространства, соответствующего методу Крейга – Бэмптона, а не собственными векторами исходной системы.

Стоит отметить, что перечисленные выше шаги по редуцированию КЭ модели производятся в КЭ комплексе (см. подраздел «Генерация файлов в КЭ комплексах для ПК EULER»).

После процедуры ортонормализации твердотельным формам будут соответствовать нулевые частоты, данные формы должны быть обязательно исключены на этапе импорта редуцированной модели (см. главу «Импорт редуцированной модели в ПК EULER»). Кроме того, каждой форме деформации соответствует определенная частота и теперь любая из них может быть при необходимости исключена, например, высокочастотные формы, которые в реальных механических системах быстро демпфируются.